As (probably most) of you know, there will be a total solar eclipse on 21 August, 2017. This will be the first such eclipse in the United States since 1979, and will be the last until 2024. If you are anything like me, you are now thinking "where do I watch this thing?". There are several maps of the path out there, and I'll get to that, but there is a different question that this post will try to answer: "where is the best place to watch this thing?" By best, I mean where the view is least likely to be obscured by clouds.
The data
The data I used for this project is historical cloud cover from the Global Data Assimilation System (GDAS) archive, which comes in the form of the cloud cover percentage every three hours in a grid of latitudes and longitudes. I pulled all of the U.S. data within one week of 21 August for every year from 1979 to 2010, all of the available years. I then compiled all of the data from 18:00:00 UTC, the closest time grid to the time of the eclipse, at each grid point.
I initially thought I would plot the average cloud cover at each grid point, and the one with the lowest average that falls within the eclipse path is the "best" location. Of course, that approach involves the assumption that the average is a good descriptor of the historical cloud cover distribution. Put another way, it assumes the cloud cover over a given grid point follows a roughly Gaussian distribution, or at least a symmetric and singly-peaked one. As you can see in the plot below, it is not:
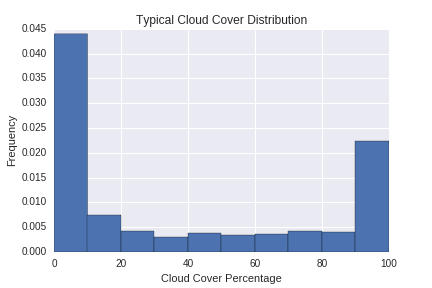
The cloud cover distribution tends to peak at 0 (clear skies) and 100 (overcast). There are therefore two statistics I will plot to decide where clouds are least likely to hinder your eclipse viewing experience.
-
"How likely is it to be completely clear?", or the fraction of historical data with cloud cover under 25%.
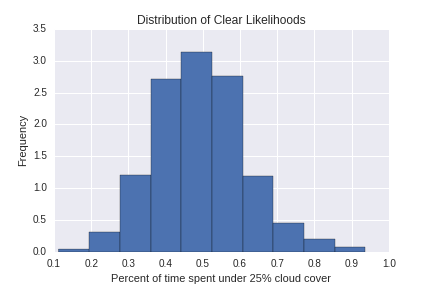
-
"How likely is it to be overcast", or the fraction of historical data with cloud cover over 75%.
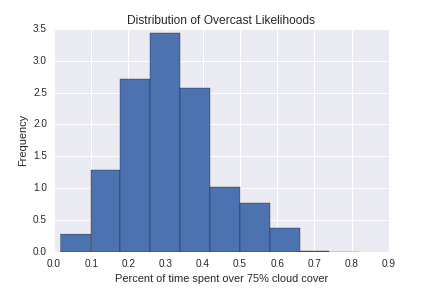
Both of the plots above are distributions across all grid points, and do follow a roughly Gaussian distribution. So I'll plot those.
So, where should I watch the eclipse?
The two plots below show the likelihood of clear/cloudy skies. They are plotted such that yellow = "sunny, good to go!", and dark blue = "cloudy, don't watch here!". The typical statistical uncertainty on the frequencies I plot is about 5%, and I binned the color scale such that a different color roughly indicates a statistically different value. I also plot the eclipse path with a gray shaded curve. If you are in this path, you will get to see the total solar eclipse; it lasts longer the closer to the center of the path you get.
I made both of the plots with the bokeh plotting library, and you can zoom on both of them by clicking the "wheel zoom" icon on the upper right of the plots, and then scrolling your mouse wheel.
Map of Clear Skies
Map of Cloudy Skies
The most striking feature of both plots is sunny California, which is very likely to be clear (\(\sim 80\%\) chance) and very unlikely to be overcast (\(<10\%\)). Unfortunately for Californians, the eclipse misses you! The best part of the country where the eclipse is visible is Oregon and Idaho. The Payette National Forest looks like a great place to watch the eclipse, with a \(66\%\) chance of clear skies and an only \(20\%\) chance of overcast skies.
Generally speaking, the Midwest states (Nebraska, Kansas, and Missouri) are pretty equally good for watching the eclipse. The probability of getting overcast skies is about \(25\%\) throughout. Moving into the Southern states (Kentucky, Tennessee, and South Carolina), that chance goes up to about \(30\%\) while the chances of a clear sky fall below \(50\%\).
I hope this helps you decide where to watch the total solar eclipse this August. Since the eclipse falls on a Monday, you will likely have to take the day off to see it unless you are lucky enough to fall in the path of totality. For any readers in Kansas City, I sure hope you at least go outside and look up that day (with protective glasses of course)!